この記事では、「ルート計算って何？」という疑問から始まり、Pythonの math モジュールの sqrt 関数を使った基本的な方法、そしてより洗練されたテクニックに至るまで、段階的にご案内します。
もしあなたが「数学は苦手だ」と感じていても心配はいりません。
私たちは、数値の0.5乗を使って、追加のライブラリなしで平方根を見つけるシンプルな方法から、forループを駆使して一連の数値の平方根を計算するプロセスを、実際のコード例と共に解説します。
Pythonでの数値計算の精度を高める方法、特に decimal モジュールの魔法を紹介し、これらの微妙な誤差を最小限に抑えるコツを探ります。
最後には、ルート計算がどのように実際のプログラミング問題、例えば2次方程式の解を見つけるためにどのように応用されるのかを体験します。
この記事を通じて、あなたはただのコードを打ち込む人から、数学的な問題を解決するためのPythonの力を使いこなすプログラマーへと変貌します。
時短でプログラミングを身に付けたいという方は、【完全無料】０円で学べるプログラミングスクールを紹介や【超厳選】20代におすすめのプログラミングスクール3選！を参考にしてください。
Pythonでルート計算をする基本
Pythonは、数学的な問題を解くための強力なプログラミング言語です。
ルート計算もPythonを使用して簡単に行うことができます。
ルート計算とは？基本を理解しよう
ルート計算、つまり平方根を見つけることは、数学における基本的な操作の一つです。
これは、ある数xのルート（平方根）を求めるときに、その数を2回かけ合わせるとxになる数を指します。例えば、9のルートは3です。
# Pythonで9の平方根を計算する
import math
root_of_nine = math.sqrt(9)
print(root_of_nine) # 結果は3このような計算は、科学計算やエンジニアリングの問題解決において、非常に重要です。
Pythonのmathモジュールを使ったルート計算
Pythonでルート計算を行うための最も一般的な方法は、math モジュールの sqrt 関数を使用することです。
これは、Pythonの標準ライブラリに含まれるモジュールで、平方根を計算するための専用の関数が用意されています。
# mathモジュールをインポート
import math
# 平方根を計算する
number = 16
root = math.sqrt(number)
print(f"The square root of {number} is {root}.")このコードは、16の平方根を求め、それが4であることを出力します。
**0.5を使ったルート計算のテクニック
Pythonでは、べき乗演算子 ** を使用して、数値の0.5乗を計算することで平方根を求めることができます。
これは、math モジュールを使わずに同様の結果を得る便利なショートカットです。
# 0.5乗を使って平方根を計算する
number = 16
root = number ** 0.5
print(f"The square root of {number} is {root}.")このコードは、先程の math.sqrt と同じく、16の平方根が4であることを出力します
Pythonでのルート計算の応用
Pythonの能力は基本的な数学演算にとどまらず、複雑な数学的問題や実際のアプリケーションにおいてもその真価を発揮します。
複数の数値のルートを計算する
特定の数列に対して平方根を計算するには、for ループを使うと効率的です。
これにより、コードの再利用性が高まり、一連の数値に対して同一の操作を簡単に適用できます。
# 1から10までの数値の平方根を計算する
import math
for number in range(1, 11):
root = math.sqrt(number)
print(f"The square root of {number} is {root}.")このコードは、1から10までの各数に対してその平方根を計算し、結果を出力します。
ルート計算の誤差とその対処法
ルート計算を行う際には、コンピューターの数値の表現制限により誤差が生じることがあります。
これは特に、無理数の平方根を扱う際に良く起きる現象です。
Pythonでこのような誤差を最小化するには、decimal モジュールの使用が一つの解決策です。
from decimal import Decimal, getcontext
# 誤差を減らすために小数点以下の精度を設定
getcontext().prec = 100
# Decimalを使って平方根を計算する
number = Decimal('2')
root = number.sqrt()
print(f"The square root of 2 is approximately {root}.")このコードは、Decimalクラスを使用して2の平方根を高い精度で計算します。
実践的なルート計算例
実際のプログラムでは、ルート計算が、例えば2次方程式の解の計算など、より複雑な数学的演算の一部として組み込まれることがあります。
import math
# 2次方程式 ax^2 + bx + c = 0 の解を計算する
a = 1
b = -5
c = 6
# 判別式を計算する
discriminant = b**2 - 4*a*c
# 解を計算する
root1 = (-b + math.sqrt(discriminant)) / (2*a)
root2 = (-b - math.sqrt(discriminant)) / (2*a)
print(f"The solutions are {root1} and {root2}.")このコードは、係数が1, -5, 6の2次方程式の解を計算し、出力します。
おすすめのプログラミングスクール
誰にでもおすすめできるプログラミングスクールは、TechAcademy（テックアカデミー）です。
他のプログラミングスクールにはないUnityコースがあるのでメタバースを開発するためには最適です。
学割が多数用意されているため、大学生にもオススメのスクールです。
特徴１：合格率10%の厳しい選考を通過した優秀なメンター
TechAcademy（テックアカデミー）のメンターは、合格率10%の非常に厳しい選考を通過した方しかいません。
そのため、メンターの方へ質問をすれば確実に求めている回答が得られます。
プログラミングスクールでの習熟度は、担当するメンターに左右されますが、TechAcademy（テックアカデミー）では、どのメンターが担当になっても損したと思うことはないです。
特徴２：受講生に1人ずつ現役のプロのパーソナルメンターがつく
特徴１で挙げた優秀なメンターがマンツーマンで指導してくれます。
これほど贅沢な制度はないと思います。
受講生１人にメンターが１人つくため、質問や相談したことに対しての回答が遅れる心配もありません。
特徴３：カリキュラムを無期限で閲覧可能
受講したカリキュラムを、期限なくいつでも閲覧することが出来ます。
そのため、後で忘れてしまったときやもう一度見直して復習したいときなどに、とても役に立ちます。
Tech Academy
- 受講者数No.1のプログラミングスクール
- 通過率10%の選考に合格した優秀な講師
- カリキュラムを閲覧制限なし
- コースの種類が豊富
- オンラインで完結
- 無料体験あり
- 無料カウンセリングあり
- 学割あり
プログラミングスクールの受講料を安くする方法
プログラミングスクールの受講料を安くする方法として、「教育訓練給付制度」があります。
教育訓練給付制度は、厚生労働省指定講座を受講後、申請をすることで最大７０％（上限５６万円）が給付されます。
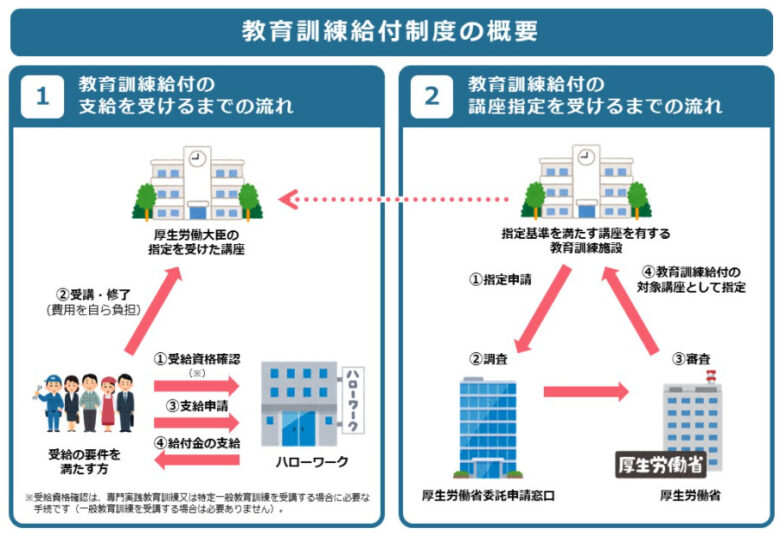
国がこんなにもお得な制度を用意してくれています。これを使わないのは損です。
情報は武器です。お得な制度は積極的に活用しましょう。
Pythonでルート計算の達人になろう
Pythonを使ったルート計算は、プログラミングの基礎であり、初心者でも容易に習得できる重要なスキルです。
この記事では、その基本から応用までを網羅し、プログラミング初心者でも理解しやすいように解説しました。
以下に重要なポイントをまとめます。
Pythonでのルート計算の基礎をしっかり押さえることは、複雑なアルゴリズムやデータ分析を扱う上で不可欠です。
この記事を通じて、Pythonでの効率的なルート計算方法を身に付け、より高度なプログラミング技術への道を切り開くことをお勧めします。
